Алгебра та геометрія 11 клас
Завдання з алгебри і початків аналізу
від 13.04.2020р. (виконати до 17.04.2020р.)посилання
Самостійна робота з геометрії
(це, лише зразок, а не повний розв'язок завдання 4)
Як побачити завдання, просто натискаєш на своє прізвище і ти бачиш всього три завдання з арифметики, алгебри і геометрії (кожне завдання оцінюється в 4 бали).
БАЖАЮ УСПІХІВ!
2.
БабічДарина
3.
БехтерМарія
8.
ЄфремоваЄва
9.
ЖуковДмитро
11. Кошель Ілля
13. Кулініч Аліна
15. Лунякін Михайло
17. Мелащенко Андрій
20. Пеленко Дмитро
21. Ракша Ксенія
22. Русев Дмитро
23. Сажин Владислав
24. Соболь Олександр
25. Сухенко Валерія
26. Тімошкін Дмитро
27. Тунік Олександр
28. Харчілава Тимур
29. Хоменко Карина
30. Чалий Віталій
Посилання на відео урок з теми
Вибіркові характеристики: розмах вибірки, мода,медіана, середнє значення
Посилання на відео урок з теми
Куля і сфера
Самостійна робота (АЛГЕБРА) № 1
з теми "Корінь n-го степеня. Степеневі функції"
Посилання на підручник
«Математика (алгебра і початки аналізу та геометрія, рівень стандарту)» підручник для 10 класу закладів загальної середньої освіти
Готуємося до Державної Підсумкової Атестації
ЗАТВЕРДЖУЮ
директор департаменту загальної
середньої та дошкільної освіти
Міністерства освіти і науки України
Ю. Г. Кононенко
директор департаменту загальної
середньої та дошкільної освіти
Міністерства освіти і науки України
Ю. Г. Кононенко
Математика
Державна
підсумкова атестація з математики проводиться за програмами,
затвердженими Міністерством освіти і науки України, а саме: «Математика. 5-9
класи» та «Навчальна програма для поглибленого вивчення математики в 8-9 класах
загальноосвітніх навчальних закладів», розміщені на сайті МОН.
Для проведення державної підсумкової атестації
готують не менше 10 варіантів контрольних робіт (якщо кількість учнів в класі
менша 10, то по одному варіанту на кожного учня). Для учнів загальноосвітніх
класів пропонується поділити роботу на 3 частини.
Перша
частина –
10-12 завдань у тестовій формі з однією правильною відповіддю на кожне
завдання. Для кожного тестового завдання рекомендується подати 4-5 варіантів
відповіді. Завдання з вибором відповіді вважається виконаним правильно, якщо в
роботі указана тільки одна літера, якою позначена правильна відповідь. При
цьому учень не повинен наводити будь-які міркування, що пояснюють його вибір.
Друга
частина атестаційної
роботи може складатися із 4-6 завдань відкритої форми з короткою відповіддю.
Такі завдання вважаються виконаними правильно, якщо записана правильна
відповідь (наприклад: число, вираз, корені рівняння тощо). Усі необхідні
обчислення, перетворення тощо учні виконують на чернетках.
Третя
частина атестаційної
роботи може складатися з 3-4 завдань відкритої форми з розгорнутою відповіддю.
Завдання третьої частини вважаються виконаними правильно, якщо учень навів
розгорнутий запис розв’язування завдання з обґрунтуванням кожного етапу розв'язку
та надав правильну відповідь. Правильність виконання завдань третьої частини
оцінює вчитель відповідно до критеріїв і схеми оцінювання завдань з якими учні
завчасно ознайомлені.
Для
класів з поглибленим вивченням математики пропонується додати четверту
частину роботи. Її рекомендується скласти із 3 завдань, що відповідають
програмі поглибленого вивчення математики.
У
кожній із частин атестаційної роботи рекомендується поєднати завдання з алгебри
і геометрії у орієнтовному відношенні 2 до 1. Також завдання мають охоплювати
весь курс математики 5-9 класу.
Завдання третьої та четвертої частин
атестаційної роботи учні виконують на аркушах зі штампом відповідного
загальноосвітнього навчального закладу.
Державна
підсумкова атестація з математики проводиться протягом 135 хв. для учнів
загальноосвітніх класів.
Учні
класів з поглибленим вивченням математики виконують атестаційну роботу протягом
180 хвилин.
При
оцінюванні письмової роботи необхідно користуватися критеріями оцінювання
затвердженими наказом МОН від 21.08.2013 № 1222 «Про затвердження орієнтовних вимог
оцінювання навчальних досягнень учнів із базових дисциплін у системі загальної
середньої освіти». Систему переведення балів у оцінку обґрунтовують і
оприлюднюють.
Структура, зміст та оцінювання завдань атестаційної роботи
На основі вимог до
проведення державної підсумкової атестації у закладах загальної середньої
освіти 2017/2018 навчальному році Лист № 1/9-185 від 27 березня 2018 року та за
збірником рекомендованим Міністерством освіти і науки України «Збірник завдань
для держаної підсумкової атестації з математики. 9 клас» автори: О.І. Глобін,
О.В. Єргіна, П.Б. Сидоренко, О.В. Комаренко Київ: Центр навчально-методичної
літератури, 2013 р. складено завдання і критерії оцінювання.
У першій частині кожної атестаційної роботи
пропонується 12 завдань з вибором однієї правильної відповіді. До кожного
завдання наведено чотири можливі варіанти відповіді, з яких тільки одна є
правильною. Завдання з вибором однієї відповіді вважається виконаним
правильно, якщо в бланку відповідей указано
тільки одну літеру, якою позначена правильна відповідь. При цьому учень не
повинен наводити будь-яких міркувань, що пояснюють його вибір.
Розподіл завдань першої частини за класами, предметами та
рівнями складності наведено в таблиці 1.
Таблиця 1
Номер завдання
|
Відповідність завдання класу навчання
|
Предмет
|
Відповідність завдання рівню навчальних досягнень учнів
|
Примітка
|
1.1
|
5 кл.
|
математика
|
початковий або середній
|
Одне із завдань 1.1, 1.2 початкового рівня, а інше - середнього
|
1.2
|
6 кл.
|
математика
|
початковий або середній
|
|
1.3
|
7 кл.
|
алгебра
|
початковий
|
|
1.4
|
7 кл.
|
алгебра
|
середній
|
|
1.5
|
8 кл.
|
алгебра
|
початковий
|
|
1.6
|
8 кл.
|
алгебра
|
середній
|
|
1.7
|
9 кл.
|
алгебра
|
початковий
|
|
1.8
|
9 кл.
|
алгебра
|
середній
|
|
1.9
|
7 кл.
|
геометрія
|
початковий або середній
|
Одне із завдань 1.9, 1.10 початкового рівня, а інше - середнього
|
1.10
|
8 кл.
|
геометрія
|
початковий або середній
|
|
1.11
|
9 кл.
|
геометрія
|
початковий
|
|
1.12
|
9 кл.
|
геометрія
|
середній
|
Правильне розв’язання кожного завдання першої частини
1.1–1.12 оцінюється одним балом. Якщо у бланку відповідей указано правильну
відповідь, то за це завдання нараховується 1 бал, якщо ж указана учнем
відповідь є неправильною, то виконання завдання оцінюється у 0 балів.
Друга частина атестаційної роботи складається із 4 завдань
відкритої форми з короткою відповіддю. Завдання цієї частини вважається
виконаним правильно, якщо в бланку відповідей записана тільки правильна
відповідь (наприклад, число, вираз, корені рівняння тощо). Усі необхідні
обчислення, перетворення тощо учні виконують на чернетках.
Розподіл завдань другої частини за класами, предметами та рівнями складності
наведено у таблиці 2.
Таблиця 2
Номер завдання
|
Відповідність завдання класу навчання
|
Предмет
|
Відповідність завдання рівню навчальних досягнень учнів
|
2.1
|
7 – 9 кл.
|
алгебра
|
достатній
|
2.2
|
7 – 9 кл.
|
алгебра
|
достатній
|
2.3
|
7 – 9 кл.
|
алгебра
|
достатній
|
2.4
|
7 – 9 кл.
|
геометрія
|
достатній
|
Правильне розв’язання кожного із завдань 2.1–2.4 оцінюється двома балами:
якщо у бланку відповідей указано правильну відповідь до завдання, то за це
нараховується 2 бали, якщо ж указана учнем відповідь є неправильною, то бали за
таке завдання не нараховуються. Часткове виконання завдання другої частини
(наприклад, якщо учень правильно знайшов один з двох коренів рівняння або
розв’язків системи рівнянь) оцінюється 1 балом.
Якщо учень вважає за потрібне внести зміни у відповідь до якогось із
завдань першої чи другої частини, то він має це зробити у спеціально відведеній
для цього частині бланка. Таке виправлення не веде до втрати балів. Якщо ж
виправлення зроблено в основній частині бланка відповідей, то бали за таке
завдання не нараховуються.
Третя частина атестаційної роботи
складається із завдань відкритої форми з розгорнутою відповіддю. Такі
завдання вважаються виконаними правильно, якщо учень навів розгорнутий запис
розв’язування з обґрунтуванням кожного його етапу та дав правильну відповідь.
Завдання третьої частини атестаційної роботи учень виконує на аркушах зі
штампом відповідного загальноосвітнього навчального закладу. Формулювання
завдань третьої частини учень не переписує, а вказує тільки номер завдання.
Третя частина атестаційної роботи містить три завдання. Розподіл завдань третьої
частини за класами, предметами та рівнями складності наведено відповідно у
таблиці 3.
Таблиця 3
Номер завдання
|
Відповідність завдання класу навчання
|
Предмет
|
Відповідність завдання рівню навчальних досягнень учнів
|
Примітка
|
3.1
|
7 – 9 кл.
|
алгебра
|
достатній
|
Текстова
задача, що розв’язується за допомогою рівняння або системи рівнянь
|
3.2
|
7 – 9 кл.
|
алгебра
|
високий
|
|
3.3
|
7 – 9 кл.
|
геометрія
|
високий
|
Правильне розв’язання завдання 3.1 оцінюється чотирма балами, а кожне із
завдань 3.2, 3.3 – шістьма балами.
Для оцінювання в балах завдань третьої частини атестаційної роботи
пропонується користуватися критеріями, наведеними в таблиці 4.
Таблиця 4
Що виконав учень
|
Відповідна кількість балів за завдання
|
||
Максимальний бал – 6
|
Максимальний бал – 4
|
||
|
6 балів
|
4 бали
|
|
|
5 балів
|
3 бали
|
|
Отримав відповідь, записав правильний хід розв’язування завдання, але в
процесі розв’язування припустився помилки обчислювального або логічного (при
обґрунтуванні) характеру
|
4 бали
|
||
|
3 бали
|
2 бали
|
|
|
2 бали
|
1 бал
|
|
Лише розпочав правильно розв’язувати
завдання або розпочав неправильно, але наступні етапи розв’язування виконав
правильно
|
1 бал
|
||
|
0 балів
|
0 балів
|
|
Виправлення і закреслення в оформленні розв’язання завдань третьої частини,
якщо вони зроблені акуратно, не є підставою для зниження оцінки.
Наведені критерії мають бути відомі учням.
Переведення оцінки у балах в оцінку за 12-бальною системою оцінювання
навчальних досягнень учнів
Сума балів, нарахованих за виконані учнем завдання, переводиться в оцінку
за 12-бальною системою оцінювання навчальних досягнень учнів за спеціальною
шкалою.
Для учнів загальноосвітніх класів максимально можлива сума
балів за атестаційну роботу становить 36 (див. таблицю 5).
Таблиця 5
Номер завдання
|
Кількість балів
|
Усього
|
1.1 – 1.12
|
по 1 балу
|
12 балів
|
2.1 – 2.4
|
по 2 балу
|
8 балів
|
3.1
|
4 бали
|
4 бали
|
3.2, 3.3
|
по 6 балів
|
12 балів
|
Сума балів
|
36 балів
|
|
Відповідність кількості набраних учнем балів оцінці за 12-бальною системою
оцінювання навчальних досягнень учнів наведено в таблиці 6.
Таблиця 6
Кількість набраних балів
|
Оцінка за 12 – бальною системою оцінювання навчальних досягнень учнів
|
0 – 2
|
1
|
3 – 4
|
2
|
5 – 6
|
3
|
7 – 8
|
4
|
9 – 10
|
5
|
11 – 12
|
6
|
13 – 16
|
7
|
17 – 20
|
8
|
21 – 24
|
9
|
25 – 28
|
10
|
29 – 32
|
11
|
33 – 36
|
12
|
Варіант 1 збірник ДПА математика 2018 О.С. Істер
Варіант 2 збірник ДПА математика 2018 О.С. Істер
Варіант 3 збірник ДПА математика 2018 О.С. Істер
Варіант 4 збірник ДПА математика 2018 О.С. Істер
Варіант 5 збірник ДПА математика 2018 О.С. Істер
Варіант 6 збірник ДПА математика 2018 О.С. Істер
Варіант 7 збірник ДПА математика 2018 О.С. Істер
Варіант 8 збірник ДПА математика 2018 О.С. Істер
Варіант 9 збірник ДПА математика 2018 О.С. Істер
Варіант 10 збірник ДПА математика 2018 О.С. Істер
Вiтаємо переможцiв
1.
Пеленко
Димтро – 21 б.;
2.
Мелащенко
Андрій – 21 б.;
3.
Мансурова
Маргарита – 20 б.;
4.
Хоменко
Карина – 20 б.
Вітаємо
Шановнi учнi 9 класу!
Для підготовки у участі в олімпіаді з математики пропоную відвідати ось тут.
Підручники для 9 класу з алгебри та геометрії
Геометрія https://drive.google.com/file/d/0B3m2TqBM0APKMnZvZ1RNVWNtb00/view
Алгебра https://drive.google.com/file/d/0B3m2TqBM0APKZmhaZVhiTk5GWEk/view
Готуємось до вивчення нової теми з алгебри
Тема. Означення квадратного рівняння. Неповні квадратні рівняння та їх розв'язування
Мета:
домогтися свідомого розуміння учнями означення квадратного рівняння,
зведеного квадратного рівняння, неповного квадратного рівняння, назви
коефіцієнтів квадратного рівняння; сформувати первинні вміння
формулювати означення квадратного рівняння та його видів (зведеного та
неповного), визначати коефіцієнти квадратного рівняння та за ними
визначати вид квадратного рівняння; підготувати учнів до сприйняття
наступного матеріалу (розв'язування неповних квадратних рівнянь).
Тип уроку: засвоєння знань та вмінь.
Наочність та обладнання: опорний конспект «Квадратні рівняння».
Хід уроку
І. Організаційний етап
На цьому етапі уроку слід надати учням інформацію про:
орієнтовний план вивчення розділу;
кількість навчальних годин;
приблизний зміст матеріалу;
основні вимоги до знань та вмінь учнів;
орієнтовний зміст завдань, що будуть винесені на контрольну роботу.
(Цю інформацію можна помістити на стенді «Довідково-інформаційний куточок» у кабінеті математики та запропонувати учням для самостійного ознайомлення в позаурочний час).
II. Перевірка домашнього завдання
Якщо аналіз контрольної роботи учні виконували в письмовій формі, вчитель збирає зошити на перевірку.
III. Формулювання мети і завдань уроку
З метою усвідомлення учнями логіки вивчення матеріалу, пропонуємо їм схему, що відтворює основні змістові лінії шкільного курсу алгебри та зв'язок між ними:
Число → Числовий вираз → Буквений вираз → Рівняння, нерівність → → Задача → Функція |
Підставивши в цю схему ірраціональне число та узагальнивши вивчений матеріал, доходимо до висновку, що після ознайомлення із видами і способами перетворень виразів, які містять квадратний корінь, слід перейти до вивчення всіх видів рівнянь (крім вивчених раніше рівнянь х2 = а і
IV. Актуалізація опорних знань та вмінь
З метою успішного сприйняття учнями навчального матеріалу уроку слід активізувати такі знання і вміння: поняття многочлена стандартного вигляду та його коефіцієнтів; виконання арифметичних дій з многочленами, виконання рівносильних перетворень рівнянь, виконання арифметичних дій із дійсними числами.
Виконання усних вправ
Подайте у вигляді многочлена вираз:
(х – 2)(2 + х); (х – 3)2; (у3 – у)∙у; (у – 1)(у + 2).
Чи рівносильні рівняння:
а) 3х – 2 = х + 3 і 2х – 5 = 0; б) 5х – 1 = 3х – х2 і х2 + 2х – 1 = 0;
в) 0,5х – 3 = 0 і х – 6 = 0; г) 5х2 – 10х + 25 = 0 і х2 – 2х + 5 = 0?
Обґрунтуйте відповіді.
Розв'яжіть рівняння:
а) у – 7 = 0; б) х + 0,5 = 0; в) 8х = 0; г) 2х –
е) а(а – 1) = 0; ж)
V. Засвоєння знань
План вивчення нового матеріалу
Означення квадратного рівняння. Коефіцієнти квадратного рівняння.
Зведене квадратне рівняння.
Неповне квадратне рівняння. Види неповних квадратних рівнянь.
Конспект 12 | ||||||||
Квадратні рівняння | ||||||||
1. Означення: | ||||||||
ах2 + bх + с = 0, а ≠ 0, b і с — будь-які дійсні числа | ||||||||
↓ Квадратні рівняння 2. Види квадратних рівнянь: | ||||||||
Неповні квадратні рівняння: | ||||||||
b = 0, ах2 + с = 0 | c = 0, ax2 + bx=0 | с = b = 0, ах2 = 0 | ||||||
Якщо b = 0 або с = 0 або b = с = 0 ↑ | ||||||||
ах2 + bx + c =0, а ≠ 0 | ||||||||
↓ Якщо а = 1 | ||||||||
Зведене квадратне рівняння | ||||||||
х2 + px + q = 0 | ||||||||
3. Розв'язування квадратних рівнянь | ||||||||||
а) Неповні квадратні рівняння: | ||||||||||
с = 0, ax2 + bx = 0, х(ах + b) = 0, x = 0 або aх + b = 0. Завжди два корені: x = 0, | b = 0, ах2 + с = 0, ах2 = – с, Якщо | ах2 = 0, х = 0. Завжди один корінь х = 0 | ||||||||
б) Квадратні рівняння загального вигляду: | ||||||||||
ах2 + bх + с = 0, а ≠ 0 | ||||||||||
↓ | ||||||||||
Дискримінант | ||||||||||
D = b2 – 4ac | Якщо b = 2k, k | |||||||||
↓ ↓ ↓ | ||||||||||
Якщо D < 0 (D1< 0) | Якщо D = 0 (D1 = 0) | Якщо D > 0 (D1 > 0) | ||||||||
дійсних коренів немає | ||||||||||
4. Властивості коренів квадратних рівнянь: | ||||||||||
а) х2 + рх + q = 0 має корені, то  | ||||||||||
б) ах2 + bх + с = 0 має корені, то  | ||||||||||
Формулюючи означення квадратного рівняння (як рівняння виду
ах2 + bх + с = 0,
де а ≠ 0), щоб попередити помилки у визначенні коефіцієнтів квадратного рівняння, важливо вказати учням на той факт, що:
знаки «+» у записі лівої частини рівняння лише показують, що ліва частина рівняння є многочленом (тобто сумою одночленів). Тому коефіцієнти квадратного рівняння визначаються так само, як і коефіцієнти многочлена стандартного вигляду (бажано поновити в пам'яті учнів ці знання під час розв'язування відповідних усних вправ на етапі актуалізації знань);
усі коефіцієнти квадратного рівняння (крім а) можуть набувати будь-яких дійсних значень (в тому числі можуть бути нулем). Тому, щоб учні не мали проблем, сприймаючи поняття неповного квадратного рівняння, на початку знайомства з поняттям квадратного рівняння слід запропонувати достатню кількість прикладів квадратних рівнянь, коефіцієнти яких набувають різних за знаком та видом значень.
Для розуміння означень видів квадратних рівнянь важливо, щоб учні засвоїли назви коефіцієнтів квадратного рівняння. Цьому сприятиме багаторазове повторення матеріалу під час виконання усних і письмових вправ.
Уявлення про види квадратних рівнянь формується за традиційною схемою. Ці види виділяються під час розгляду особливих випадків коефіцієнтів квадратного рівняння.
VI. Формування вмінь
Виконання усних вправ
Укажіть серед поданих рівнянь квадратні: а) 5х – 2 = 0;
б) х2 – х + 1 = 0; в) х3 – х = 0; г) 5х2 + х = 0.
Для квадратних рівнянь назвіть значення їх коефіцієнтів.
Серед рівнянь виберіть:
3х2 – 2х + 7 = 0;
а) зведені; б) неповні квадратні рівняння.
Запишіть рівняння у вигляді ах2 + bх + с = 0 (якщо це можливо):
-5 – 2х + х12 = 0; х2 – 3 = 0; 5х – х2 = 0.
Виконання письмових вправ
Для реалізації дидактичної мети уроку слід виконати завдання такого змісту:
Знаходження коефіцієнтів квадратною рівняння.
1) Заповніть таблицю:
Квадратне рівняння
Коефіцієнти рівняння
ах2 + bх + с = 0
а
b
с
4
1
3
-2х2 – 3х + 1 = 0
1
0
-24
3
-5
0
5х2 – 8 = 0
7
0
0
2) Укажіть у квадратному рівнянні його коефіцієнти:
а) 5х2 – 9х + 4 = 0; б) х2 + 3х – 10 = 0; в) -х2 – 8х + 1 = 0;
г) -4х2 + 5х = 0; д) 6х2 – 30 = 0; є) 9х2 = 0.
Запис квадратного рівняння із заданими коефіцієнтами. Запишіть квадратне рівняння, коефіцієнти якого дорівнюють: а) а = 2; b = -3; с = 1; б) а = 3; b = 0; с = -7; в) а = -1; b = 4; с = 5; г) а = 2; b = 0; с = 0.
Запис зведеного квадратного рівняння, рівносильного даному. Запишіть зведене квадратне рівняння, рівносильне даному:
а) 2х2 + 2х – 6 = 0; б) -4х2 – 10х + 8 = 0.
Зведення цілого рівняння до виду ах2 + bх + с = 0 шляхом тотожних перетворень.
Зведіть рівняння до виду ах2 + bх + с = 0:
a) (2x – 1)(2x + 1) = x(2x + 3); б) (3х + 2)2 = (х + 2)(x – 3);
в) (х + 1)(х + 2) = (2х – 1)(x – 2); г) (х + 3)(3х – 2) = (4х + 5)(2х – 3).
На повторення: завдання, розв'язування яких передбачає виділення повного квадрата двочлена з квадратного тричлена.
Логічні вправи та завдання підвищеного рівня складності для учнів, які мають достатній та високий рівні знань.
2) Видаліть зайвий запис: а) 3х2 – 5x + 1 = 0; б) х2 – 4х = 0;
в) (х – 1)2 – (3х – 1)2 = 0; г) (х – 1)2 – (х + 2)2 = 0.
Мета перших 4-х видів письмових завдань (див. вище) — домогтися засвоєння учнями означення квадратного рівняння та його різновидів, сформувати в учнів уміння правильно називати та визначати коефіцієнти квадратного рівняння, а також повторити види рівносильних перетворень рівнянь та поновити в пам'яті способи дій під час виконання цих перетворень. Завдання на повторення мають на меті підготувати учнів до сприйняття ними матеріалу наступного розділу «Формула коренів квадратного рівняння».
VII. Підсумки уроку
В якому випадку правильно визначено коефіцієнти?
У рівнянні 5х + х2 – 4 = 0 коефіцієнти a, b, c відповідно дорівнюють:
а) 1; 5; -4; б) 5; 1;-4; в) -4; 5; 1; г) 1; -4; 5.
VIII. Домашнє завдання
Вивчити зміст теоретичного матеріалу уроку.
Розв'язати вправи на закріплення вивченого матеріалу (аналогічних за змістом до вправ класної роботи).
На повторення: вправи на виділення повного квадрата двочлена.
тема "Третий признак равенства треугольников"
смотри видео
а вот еще одно видео из реальной школы (почему то мне это видео больше понравилось)
В помощь готовящимся к докладу о ЗОЛОТОМ СЕЧЕНИИ
Золотое сечение – математика
Человек
различает окружающие его предметы по форме. Интерес к форме какого-либо
предмета может быть продиктован жизненной необходимостью, а может быть
вызван красотой формы. Форма, в основе построения которой лежат
сочетание симметрии и золотого сечения, способствует наилучшему
зрительному восприятию и появлению ощущения красоты и гармонии. Целое
всегда состоит из частей, части разной величины находятся в определенном
отношении друг к другу и к целому. Принцип золотого сечения – высшее
проявление структурного и функционального совершенства целого и его
частей в искусстве, науке, технике и природе.
Золотое сечение – гармоническая пропорция
В математике пропорцией (лат. proportio) называют равенство двух отношений:a : b = c : d.
Отрезок прямой АВ можно разделить на две части следующими способами:
на две равные части – АВ : АС = АВ : ВС;
на две неравные части в любом отношении (такие части пропорции не образуют);
таким образом, когда АВ : АС = АС : ВС.
Последнее и есть золотое деление или деление отрезка в крайнем и среднем отношении.
Золотое
сечение – это такое пропорциональное деление отрезка на неравные части,
при котором весь отрезок так относится к большей части, как сама
большая часть относится к меньшей; или другими словами, меньший отрезок
так относится к большему, как больший ко всему
a : b = b : c или с : b = b : а.
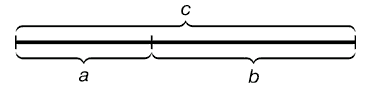 Рис. 1. Геометрическое изображение золотой пропорции
Практическое знакомство с золотым сечением начинают с деления отрезка прямой в золотой пропорции с помощью циркуля и линейки.
Рис. 1. Геометрическое изображение золотой пропорции
Практическое знакомство с золотым сечением начинают с деления отрезка прямой в золотой пропорции с помощью циркуля и линейки.
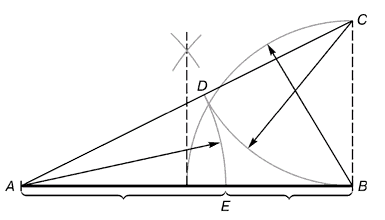 Рис. 2. Деление отрезка прямой по золотому сечению. BC = 1/2 AB; CD = BC
Из точки
В восставляется перпендикуляр, равный половине АВ. Полученная точка С
соединяется линией с точкой А. На полученной линии откладывается отрезок
ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ.
Полученная при этом точка Е делит отрезок АВ в соотношении золотой
пропорции.
Отрезки
золотой пропорции выражаются бесконечной иррациональной дробью AE =
0,618…, если АВ принять за единицу, ВЕ = 0,382… Для практических целей
часто используют приближенные значения 0,62 и 0,38. Если отрезок АВ
принять за 100 частей, то большая часть отрезка равна 62, а меньшая – 38
частям.
Свойства золотого сечения описываются уравнением:
Рис. 2. Деление отрезка прямой по золотому сечению. BC = 1/2 AB; CD = BC
Из точки
В восставляется перпендикуляр, равный половине АВ. Полученная точка С
соединяется линией с точкой А. На полученной линии откладывается отрезок
ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ.
Полученная при этом точка Е делит отрезок АВ в соотношении золотой
пропорции.
Отрезки
золотой пропорции выражаются бесконечной иррациональной дробью AE =
0,618…, если АВ принять за единицу, ВЕ = 0,382… Для практических целей
часто используют приближенные значения 0,62 и 0,38. Если отрезок АВ
принять за 100 частей, то большая часть отрезка равна 62, а меньшая – 38
частям.
Свойства золотого сечения описываются уравнением:
x2 – x – 1 = 0.
Решение этого уравнения:
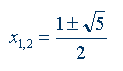 Свойства золотого сечения создали вокруг этого числа романтический ореол таинственности и чуть ли не мистического поклонения.
Второе золотое сечение
Болгарский
журнал «Отечество» (№10, 1983 г.) опубликовал статью Цветана
Цекова-Карандаша «О втором золотом сечении», которое вытекает из
основного сечения и дает другое отношение 44 : 56.
Свойства золотого сечения создали вокруг этого числа романтический ореол таинственности и чуть ли не мистического поклонения.
Второе золотое сечение
Болгарский
журнал «Отечество» (№10, 1983 г.) опубликовал статью Цветана
Цекова-Карандаша «О втором золотом сечении», которое вытекает из
основного сечения и дает другое отношение 44 : 56.
Такая пропорция
обнаружена в архитектуре, а также имеет место при построении композиций
изображений удлиненного горизонтального формата.
Деление
осуществляется следующим образом. Отрезок АВ делится в пропорции
золотого сечения. Из точки С восставляется перпендикуляр СD. Радиусом АВ
находится точка D, которая соединяется линией с точкой А. Прямой угол
АСD делится пополам. Из точки С проводится линия до пересечения с линией
AD. Точка Еделит отрезок AD в отношении 56 : 44.
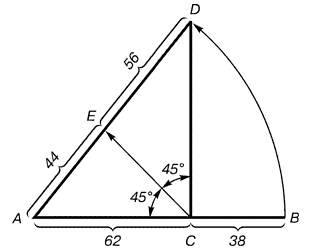 Рис. 3. Построение второго золотого сечения
Рис. 3. Построение второго золотого сечения
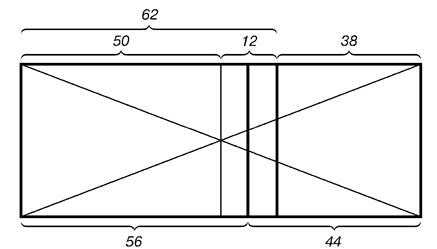 Рис. 4. Деление прямоугольника линией второго золотого сечения
На
рисунке показано положение линии второго золотого сечения. Она находится
посередине между линией золотого сечения и средней линией
прямоугольника.
Золотой треугольник
Для нахождения отрезков золотой пропорции восходящего и нисходящего рядов можно пользоваться пентаграммой.
Рис. 4. Деление прямоугольника линией второго золотого сечения
На
рисунке показано положение линии второго золотого сечения. Она находится
посередине между линией золотого сечения и средней линией
прямоугольника.
Золотой треугольник
Для нахождения отрезков золотой пропорции восходящего и нисходящего рядов можно пользоваться пентаграммой.
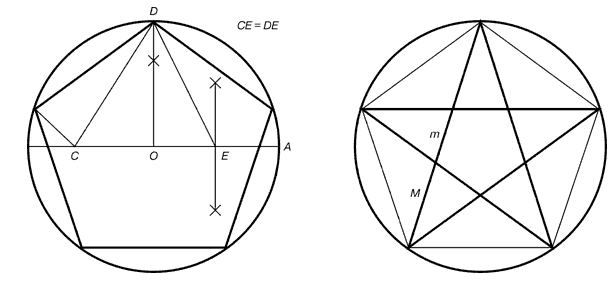 Рис. 5. Построение правильного пятиугольника и пентаграммы
Для
построения пентаграммы необходимо построить правильный пятиугольник.
Способ его построения разработал немецкий живописец и график Альбрехт
Дюрер (1471…1528). Пусть O – центр окружности, A – точка на окружности и
Е – середина отрезка ОА. Перпендикуляр к радиусу ОА, восставленный в
точке О, пересекается с окружностью в точке D. Пользуясь циркулем,
отложим на диаметре отрезок CE = ED. Длина стороны вписанного в
окружность правильного пятиугольника равна DC. Откладываем на окружности
отрезки DC и получим пять точек для начертания правильного
пятиугольника. Соединяем углы пятиугольника через один диагоналями и
получаем пентаграмму. Все диагонали пятиугольника делят друг друга на
отрезки, связанные между собой золотой пропорцией.
Рис. 5. Построение правильного пятиугольника и пентаграммы
Для
построения пентаграммы необходимо построить правильный пятиугольник.
Способ его построения разработал немецкий живописец и график Альбрехт
Дюрер (1471…1528). Пусть O – центр окружности, A – точка на окружности и
Е – середина отрезка ОА. Перпендикуляр к радиусу ОА, восставленный в
точке О, пересекается с окружностью в точке D. Пользуясь циркулем,
отложим на диаметре отрезок CE = ED. Длина стороны вписанного в
окружность правильного пятиугольника равна DC. Откладываем на окружности
отрезки DC и получим пять точек для начертания правильного
пятиугольника. Соединяем углы пятиугольника через один диагоналями и
получаем пентаграмму. Все диагонали пятиугольника делят друг друга на
отрезки, связанные между собой золотой пропорцией.
Каждый конец
пятиугольной звезды представляет собой золотой треугольник. Его стороны
образуют угол 36° при вершине, а основание, отложенное на боковую
сторону, делит ее в пропорции золотого сечения.
Проводим
прямую АВ. От точки Аоткладываем на ней три раза отрезок Опроизвольной
величины, через полученную точку Р проводим перпендикуляр к линии АВ, на
перпендикуляре вправо и влево от точки Р откладываем отрезки О.
Полученные точки d и d1 соединяем прямыми с точкой А. Отрезок dd1
откладываем на линию Ad1, получая точку С. Она разделила линию Ad1 в
пропорции золотого сечения. Линиями Ad1 и dd1 пользуются для построения
«золотого» прямоугольника.
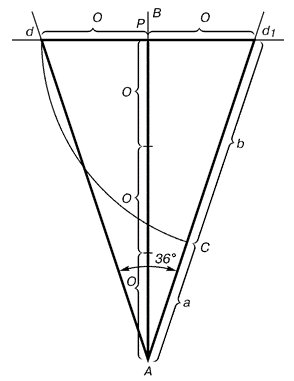 Рис. 6. Построение золотого треугольника
Рис. 6. Построение золотого треугольника
История золотого сечения
Принято
считать, что понятие о золотом делении ввел в научный обиход Пифагор,
древнегреческий философ и математик (VI в. до н.э.). Есть предположение,
что Пифагор свое знание золотого деления позаимствовал у египтян и
вавилонян. И действительно, пропорции пирамиды Хеопса, храмов,
барельефов, предметов быта и украшений из гробницы Тутанхамона
свидетельствуют, что египетские мастера пользовались соотношениями
золотого деления при их создании. Французский архитектор Ле Корбюзье
нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе,
изображающем фараона Рамзеса, пропорции фигур соответствуют величинам
золотого деления. Зодчий Хесира, изображенный на рельефе деревянной
доски из гробницы его имени, держит в руках измерительные инструменты, в
которых зафиксированы пропорции золотого деления.
Греки были
искусными геометрами. Даже арифметике обучали своих детей при помощи
геометрических фигур. Квадрат Пифагора и диагональ этого квадрата были
основанием для построения динамических прямоугольников.
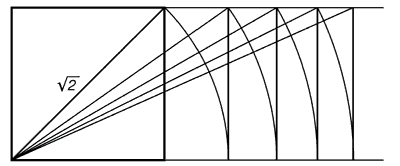 Рис. 7. Динамические прямоугольники
Платон
(427…347 гг. до н.э.) также знал о золотом делении. Его диалог «Тимей»
посвящен математическим и эстетическим воззрениям школы Пифагора и, в
частности, вопросам золотого деления.
Рис. 7. Динамические прямоугольники
Платон
(427…347 гг. до н.э.) также знал о золотом делении. Его диалог «Тимей»
посвящен математическим и эстетическим воззрениям школы Пифагора и, в
частности, вопросам золотого деления.
В фасаде древнегреческого
храма Парфенона присутствуют золотые пропорции. При его раскопках
обнаружены циркули, которыми пользовались архитекторы и скульпторы
античного мира. В Помпейском циркуле (музей в Неаполе) также заложены
пропорции золотого деления.
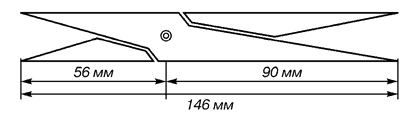 Рис. 8. Античный циркуль золотого сечения
В
дошедшей до нас античной литературе золотое деление впервые упоминается в
«Началах» Евклида. Во 2-й книге «Начал» дается геометрическое
построение золотого деления После Евклида исследованием золотого деления
занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др. В
средневековой Европе с золотым делением познакомились по арабским
переводам «Начал» Евклида. Переводчик Дж. Кампано из Наварры (III в.)
сделал к переводу комментарии. Секреты золотого деления ревностно
оберегались, хранились в строгой тайне. Они были известны только
посвященным.
Рис. 8. Античный циркуль золотого сечения
В
дошедшей до нас античной литературе золотое деление впервые упоминается в
«Началах» Евклида. Во 2-й книге «Начал» дается геометрическое
построение золотого деления После Евклида исследованием золотого деления
занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др. В
средневековой Европе с золотым делением познакомились по арабским
переводам «Начал» Евклида. Переводчик Дж. Кампано из Наварры (III в.)
сделал к переводу комментарии. Секреты золотого деления ревностно
оберегались, хранились в строгой тайне. Они были известны только
посвященным.
В эпоху Возрождения усиливается интерес к золотому
делению среди ученых и художников в связи с его применением как в
геометрии, так и в искусстве, особенно в архитектуре Леонардо да Винчи,
художник и ученый, видел, что у итальянских художников эмпирический опыт
большой, а знаний мало. Он задумал и начал писать книгу по геометрии,
но в это время появилась книга монаха Луки Пачоли, и Леонардо оставил
свою затею. По мнению современников и историков науки, Лука Пачоли был
настоящим светилом, величайшим математиком Италии в период между
Фибоначчи и Галилеем. Лука Пачоли был учеником художника Пьеро делла
Франчески, написавшего две книги, одна из которых называлась «О
перспективе в живописи». Его считают творцом начертательной геометрии.
Лука
Пачоли прекрасно понимал значение науки для искусства. В 1496 г по
приглашению герцога Моро он приезжает в Милан, где читает лекции по
математике. В Милане при дворе Моро в то время работал и Леонардо да
Винчи. В 1509 г. в Венеции была издана книга Луки Пачоли «Божественная
пропорция» с блестяще выполненными иллюстрациями, ввиду чего полагают,
что их сделал Леонардо да Винчи. Книга была восторженным гимном золотой
пропорции. Среди многих достоинств золотой пропорции монах Лука Пачоли
не преминул назвать и ее «божественную суть» как выражение божественного
триединства бог сын, бог отец и бог дух святой (подразумевалось, что
малый отрезок есть олицетворение бога сына, больший отрезок – бога отца,
а весь отрезок – бога духа святого).
Леонардо да Винчи также много
внимания уделял изучению золотого деления. Он производил сечения
стереометрического тела, образованного правильными пятиугольниками, и
каждый раз получал прямоугольники с отношениями сторон в золотом
делении. Поэтому он дал этому делению название золотое сечение. Так оно и
держится до сих пор как самое популярное.
В то же время на севере
Европы, в Германии, над теми же проблемами трудился Альбрехт Дюрер. Он
делает наброски введения к первому варианту трактата о пропорциях. Дюрер
пишет. «Необходимо, чтобы тот, кто что-либо умеет, обучил этому других,
которые в этом нуждаются. Это я и вознамерился сделать».
Судя по
одному из писем Дюрера, он встречался с Лукой Пачоли во время пребывания
в Италии. Альбрехт Дюрер подробно разрабатывает теорию пропорций
человеческого тела. Важное место в своей системе соотношений Дюрер
отводил золотому сечению. Рост человека делится в золотых пропорциях
линией пояса, а также линией, проведенной через кончики средних пальцев
опущенных рук, нижняя часть лица – ртом и т.д. Известен пропорциональный
циркуль Дюрера.
Великий астроном XVI в. Иоган Кеплер назвал золотое
сечение одним из сокровищ геометрии. Он первый обращает внимание на
значение золотой пропорции для ботаники (рост растений и их строение).
Кеплер
называл золотую пропорцию продолжающей саму себя «Устроена она так, –
писал он, – что два младших члена этой нескончаемой пропорции в сумме
дают третий член, а любые два последних члена, если их сложить, дают
следующий член, причем та же пропорция сохраняется до бесконечности».
Построение
ряда отрезков золотой пропорции можно производить как в сторону
увеличения (возрастающий ряд), так и в сторону уменьшения (нисходящий
ряд).
Если на прямой произвольной длины, отложить отрезок m, рядом
откладываем отрезок M. На основании этих двух отрезков выстраиваем шкалу
отрезков золотой пропорции восходящего и нисходящего рядов
 Рис. 9. Построение шкалы отрезков золотой пропорции
В
последующие века правило золотой пропорции превратилось в академический
канон и, когда со временем в искусстве началась борьба с академической
рутиной, в пылу борьбы «вместе с водой выплеснули и ребенка». Вновь
«открыто» золотое сечение было в середине XIX в. В 1855 г. немецкий
исследователь золотого сечения профессор Цейзинг опубликовал свой труд
«Эстетические исследования». С Цейзингом произошло именно то, что и
должно было неминуемо произойти с исследователем, который рассматривает
явление как таковое, без связи с другими явлениями. Он абсолютизировал
пропорцию золотого сечения, объявив ее универсальной для всех явлений
природы и искусства. У Цейзинга были многочисленные последователи, но
были и противники, которые объявили его учение о пропорциях
«математической эстетикой».
Рис. 9. Построение шкалы отрезков золотой пропорции
В
последующие века правило золотой пропорции превратилось в академический
канон и, когда со временем в искусстве началась борьба с академической
рутиной, в пылу борьбы «вместе с водой выплеснули и ребенка». Вновь
«открыто» золотое сечение было в середине XIX в. В 1855 г. немецкий
исследователь золотого сечения профессор Цейзинг опубликовал свой труд
«Эстетические исследования». С Цейзингом произошло именно то, что и
должно было неминуемо произойти с исследователем, который рассматривает
явление как таковое, без связи с другими явлениями. Он абсолютизировал
пропорцию золотого сечения, объявив ее универсальной для всех явлений
природы и искусства. У Цейзинга были многочисленные последователи, но
были и противники, которые объявили его учение о пропорциях
«математической эстетикой».
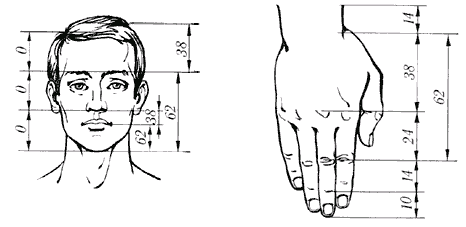 Рис. 10. Золотые пропорции в частях тела человека
Цейзинг
проделал колоссальную работу. Он измерил около двух тысяч человеческих
тел и пришел к выводу, что золотое сечение выражает средний
статистический закон. Деление тела точкой пупа – важнейший показатель
золотого сечения. Пропорции мужского тела колеблются в пределах среднего
отношения 13 : 8 = 1,625 и несколько ближе подходят к золотому сечению,
чем пропорции женского тела, в отношении которого среднее значение
пропорции выражается в соотношении 8 : 5 = 1,6. У новорожденного
пропорция составляет отношение 1 : 1, к 13 годам она равна 1,6, а к 21
году равняется мужской. Пропорции золотого сечения проявляются и в
отношении других частей тела – длина плеча, предплечья и кисти, кисти и
пальцев и т.д.
Рис. 10. Золотые пропорции в частях тела человека
Цейзинг
проделал колоссальную работу. Он измерил около двух тысяч человеческих
тел и пришел к выводу, что золотое сечение выражает средний
статистический закон. Деление тела точкой пупа – важнейший показатель
золотого сечения. Пропорции мужского тела колеблются в пределах среднего
отношения 13 : 8 = 1,625 и несколько ближе подходят к золотому сечению,
чем пропорции женского тела, в отношении которого среднее значение
пропорции выражается в соотношении 8 : 5 = 1,6. У новорожденного
пропорция составляет отношение 1 : 1, к 13 годам она равна 1,6, а к 21
году равняется мужской. Пропорции золотого сечения проявляются и в
отношении других частей тела – длина плеча, предплечья и кисти, кисти и
пальцев и т.д.
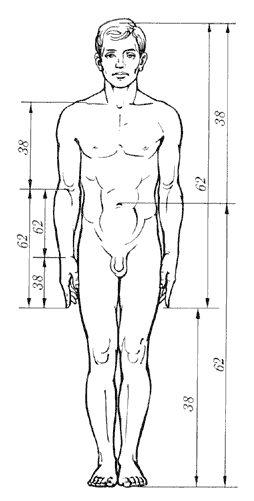
Рис. 11. Золотые пропорции в фигуре человека
Справедливость
своей теории Цейзинг проверял на греческих статуях. Наиболее подробно
он разработал пропорции Аполлона Бельведерского. Подверглись
исследованию греческие вазы, архитектурные сооружения различных эпох,
растения, животные, птичьи яйца, музыкальные тона, стихотворные размеры.
Цейзинг дал определение золотому сечению, показал, как оно выражается в
отрезках прямой и в цифрах. Когда цифры, выражающие длины отрезков,
были получены, Цейзинг увидел, что они составляют ряд Фибоначчи, который
можно продолжать до бесконечности в одну и в другую сторону. Следующая
его книга имела название «Золотое деление как основной морфологический
закон в природе и искусстве». В 1876 г. в России была издана небольшая
книжка, почти брошюра, с изложением этого труда Цейзинга. Автор укрылся
под инициалами Ю.Ф.В. В этом издании не упомянуто ни одно произведение
живописи.
В конце
XIX – начале XX вв. появилось немало чисто формалистических теории о
применении золотого сечения в произведениях искусства и архитектуры. С
развитием дизайна и технической эстетики действие закона золотого
сечения распространилось на конструирование машин, мебели и т.д.
В помощь геометрия
Отрезок прямой АВ можно разделить на две части следующими способами:
на две равные части – АВ : АС = АВ : ВС;
на две неравные части в любом отношении (такие части пропорции не образуют);
таким образом, когда АВ : АС = АС : ВС.
Последнее и есть золотое деление или деление отрезка в крайнем и среднем отношении.
Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему


x2 – x – 1 = 0.
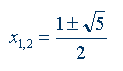
Такая пропорция обнаружена в архитектуре, а также имеет место при построении композиций изображений удлиненного горизонтального формата.



Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения.

История золотого сечения
Греки были искусными геометрами. Даже арифметике обучали своих детей при помощи геометрических фигур. Квадрат Пифагора и диагональ этого квадрата были основанием для построения динамических прямоугольников.

В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления.

В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением как в геометрии, так и в искусстве, особенно в архитектуре Леонардо да Винчи, художник и ученый, видел, что у итальянских художников эмпирический опыт большой, а знаний мало. Он задумал и начал писать книгу по геометрии, но в это время появилась книга монаха Луки Пачоли, и Леонардо оставил свою затею. По мнению современников и историков науки, Лука Пачоли был настоящим светилом, величайшим математиком Италии в период между Фибоначчи и Галилеем. Лука Пачоли был учеником художника Пьеро делла Франчески, написавшего две книги, одна из которых называлась «О перспективе в живописи». Его считают творцом начертательной геометрии.
Лука Пачоли прекрасно понимал значение науки для искусства. В 1496 г по приглашению герцога Моро он приезжает в Милан, где читает лекции по математике. В Милане при дворе Моро в то время работал и Леонардо да Винчи. В 1509 г. в Венеции была издана книга Луки Пачоли «Божественная пропорция» с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Книга была восторженным гимном золотой пропорции. Среди многих достоинств золотой пропорции монах Лука Пачоли не преминул назвать и ее «божественную суть» как выражение божественного триединства бог сын, бог отец и бог дух святой (подразумевалось, что малый отрезок есть олицетворение бога сына, больший отрезок – бога отца, а весь отрезок – бога духа святого).
Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение. Так оно и держится до сих пор как самое популярное.
В то же время на севере Европы, в Германии, над теми же проблемами трудился Альбрехт Дюрер. Он делает наброски введения к первому варианту трактата о пропорциях. Дюрер пишет. «Необходимо, чтобы тот, кто что-либо умеет, обучил этому других, которые в этом нуждаются. Это я и вознамерился сделать».
Судя по одному из писем Дюрера, он встречался с Лукой Пачоли во время пребывания в Италии. Альбрехт Дюрер подробно разрабатывает теорию пропорций человеческого тела. Важное место в своей системе соотношений Дюрер отводил золотому сечению. Рост человека делится в золотых пропорциях линией пояса, а также линией, проведенной через кончики средних пальцев опущенных рук, нижняя часть лица – ртом и т.д. Известен пропорциональный циркуль Дюрера.
Великий астроном XVI в. Иоган Кеплер назвал золотое сечение одним из сокровищ геометрии. Он первый обращает внимание на значение золотой пропорции для ботаники (рост растений и их строение).
Кеплер называл золотую пропорцию продолжающей саму себя «Устроена она так, – писал он, – что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности».
Построение ряда отрезков золотой пропорции можно производить как в сторону увеличения (возрастающий ряд), так и в сторону уменьшения (нисходящий ряд).
Если на прямой произвольной длины, отложить отрезок m, рядом откладываем отрезок M. На основании этих двух отрезков выстраиваем шкалу отрезков золотой пропорции восходящего и нисходящего рядов



Рис. 11. Золотые пропорции в фигуре человека
Любопытные и интересные факты о математике
Чем пожертвовала Софья Ковалевская ради возможности заниматься наукой?
Чтобы
получить возможность заниматься наукой, Софье Ковалевской пришлось
заключить фиктивный брак и уехать из России. В то время российские
университеты просто не принимали женщин, а чтобы эмигрировать, девушка
должна была иметь согласие отца или мужа. Так как отец Софьи был
категорически против, она вышла замуж за молодого учёного Владимира
Ковалевского. Хотя в итоге их брак стал фактическим, и у них родилась
дочь.
Почему возникла десятичная система счисления?
Используемая
нами десятичная система счисления возникла по причине того, что у
человека на руках 10 пальцев. Способность к абстрактному счёту появилась
у людей не сразу, а использовать для счёта именно пальцы оказалось
удобнее всего. Цивилизация майя и независимо от них чукчи исторически
использовали двадцатичную систему счисления, применяя пальцы не только
рук, но и ног. В основе распространённых в древних Шумере и Вавилоне
двенадцатеричной и шестидесятиричной систем тоже было использование рук:
большим пальцем отсчитывались фаланги других пальцев ладони, число
которых равно 12.
Какие оценки по математике получал Эйнштейн в школе?
Во
многих источниках, зачастую с целью ободрения плохо успевающих
учеников, встречается утверждение, что Эйнштейн завалил в школе
математику или, более того, вообще учился из рук вон плохо по всем
предметам. На самом деле всё обстояло не так: Альберт ещё в раннем
возрасте начал проявлять талант в математике и знал её далеко за
пределами школьной программы. Позднее Эйнштейн не смог поступить в
Швейцарскую высшую политехническую школу Цюриха, показав высшие
результаты по физике и математике, но не добрав нужное количество баллов
в других дисциплинах. Подтянув эти предметы, он через год в возрасте 17
лет стал студентом данного заведения.
В чем сложности?В этой рубрике речь пойдет о той теме, которую изучают семиклассники по математике, в чем же сейчас им так сложно?
Сложно в новой и очень важной теме "Одночлены и многочлены" именно она заставляет задуматься о всем материале алгебры. По этому для лучшей подготовки к этой теме предлагаю Вам - ученики и их родителям подборку видео уроков "Умножение многочлена на одночлен"
Следующий видео урок "Умножение многочлена на многочлен"
И еще один видео урок "Вынесение общего множителя за скобки"
Олимпиада
Наше победители и участники
1 место : Щедрин Иван (7-Б);
Скоробогатько Даниил (7-Б).
2 место: Гарбуз Анна (7-В).
3 место: Чернега Дарья (7-В);
Фролова Наталия (7-В).
Участники:
Артеменко Богдан;
Шамрай Никита;
Готовкин Артем;
Дендевич Евгений;
Кравец София;
Павленко Мария;
Яшин Николай.
СПАСИБО ЗА СТАРАНИЯ!
История возникновения алгебры
Суть алгебры
Алгебра,
вместе с арифметикой, есть наука о числах и через посредство чисел –
о величинах вообще. Не занимаясь изучением свойств каких-нибудь
определенных, конкретных величин, обе эти науки исследуют свойства
отвлеченных величин, как таковых, независимо от того, к каким
конкретным приложениям они способны. Различие между арифметикой и
алгеброй состоит в том, что первая наука исследует свойства данных,
определенных величин, между тем как алгебра занимается изучением
общих величин, значение которых может быть произвольное, а,
следовательно, алгебра изучает только те свойства величин, которые
общи всем величинам, независимо от их значений. Таким образом,
алгебра есть обобщенная арифметика. Это подало повод Ньютону назвать
свой трактат об алгебре "Общая арифметика". Гамильтон,
полагая, что подобно тому, как геометрия изучает свойства
пространства, алгебра изучает свойства времени, назвал алгебру
"Наукою чистого времени" – название, которое Морган
предлагал изменить на "Исчисление последовательности".
Однако такие определения не выражают ни существенных свойств алгебры,
ни исторического ее развития. Алгебру можно определить как "науку
о количественных соотношениях".
Деление алгебры
В
настоящее время, отчасти из педагогических соображений, отчасти
вследствие исторического развития этой науки, алгебру делят на низшую
и высшую. К низшей алгебре относят теорию
простейших арифметических операций над алгебраическими выражениями,
решение уравнений первой и второй степени, теорию степеней и корней,
теорию логарифмов и комбинаторику. К высшей алгебре относят теорию
уравнений произвольных степеней, теорию исключений, теорию
симметрических функций, теорию подстановок, и, наконец, изложение
различных частных способов отделения корней уравнений, определения
числа вещественных или мнимых корней данного уравнения с численными
коэффициентами, и приближённое или аналитическое (когда это возможно)
уравнений произвольных степеней.
История алгебры
Происхождение термина "алгебра"
Происхождение
самого слова "алгебра" не вполне выяснено. По мнению
большинства исследователей этого вопроса, слово "алгебра"
произошло от названия труда арабского математика Ал-Хорезми (от
самого имени которого согласно большинству исследователей происходит
популярное слово "алгоритм") "Аль-джабр-аль-мукабалла",
то есть "учение о перестановках, отношениях и решениях", но
некоторые авторы производят слово "алгебра"
от имени математика Гебера, однако само существование такого
математика подвержено сомнению.
Древнейшие сочинения по алгебре
Первое
дошедшее до нас сочинение, содержащее исследование алгебраических
вопросов, есть трактат Диофанта, жившего в середине IV века. В этом
трактате мы встречаем, например, правило знаков (минус на минус дает
плюс), исследование степеней чисел, и решение множества
неопределенных вопросов, которые в настоящее время относятся к теории
чисел. Из 13 книг, составлявших полное сочинение Диофанта, до нас
дошло только 6, в которых решаются уже довольно трудные
алгебраические задачи. Нам неизвестно о каких бы то ни было иных
сочинениях об алгебре в древности, кроме утерянного сочинения
знаменитой дочери Теона, Гипатии.
Алгебра арабов
В
Европе алгебра снова появляется только в эпоху Возрождения, и именно
от арабов. Каким образом арабы дошли до тех истин, которые мы находим
в их сочинениях, дошедших до нас в большом количестве, –
неизвестно. Они могли быть знакомы с трактатами греков, или, как
думают некоторые, получить свои знания из Индии. Сами арабы
приписывали изобретение алгебры. Магоммеду-бен-Муза, жившему около
середины IХ-го века в царствованние халифа Аль-Мамуна. Во всяком
случае, греческие авторы были известны арабам, которые собирали
древние сочинения по всем отраслям наук. Магоммед-Абульвефа перевел и
комментировал сочинения Диофанта и других предшествовавших ему
математиков (в Х веке). Но ни он, ни другие арабские математики не
внесли много нового, своего в алгебру. Они изучали ее, но не
совершенствовали.
Возрождение алгебры в Европе
Первым
сочинением, появившимся в Европе после продолжительного пробела со
времен Диофанта, считается трактат итальянского купца Леонардо,
который, путешествуя по своим коммерческим делам на Востоке,
ознакомился там с индийскими (ныне называемыми арабскими) цифрами, и
с арифметикой и алгеброй арабов. По возвращении в Италию, он написал
сочинение, охватывающее одновременно арифметику и алгебру и отчасти
геометрию. Однако сочинение это не имело большого значения в истории
науки, ибо осталось мало известным и было открыто вновь только в
середине 18-го века в одной Флорентийской
библиотеке. Между тем сочинения арабов стали проникать в Европу и
переводиться на европейские языки. Известно, например, что старейшее
арабское сочинение об алгебре Магоммеда-бен-Музы было переведено на
итальянский язык, но перевод этот не сохранился до нашего времени.
Первым известным печатным трактатом об алгебре является "Summa
de Arithmetica, Geometria, Proportioni et Proportionalita",
написанное итальянцем Лукасом дэ Бурго. Первое издание его вышло в
1494 г. и второе в 1523 г. Оно указывает нам, в каком состоянии
находилась алгебра в начале XVI века в Европе. Здесь нельзя видеть
больших успехов по сравнению с тем, что уже было известно арабам или
Диофанту. Кроме решения отдельных частных вопросов высшей арифметики,
только уравнения первой к второй степени решаются автором, и притом
вследствие отсутствия символического обозначения, все задачи и
способы их решения приходится излагать словами, чрезвычайно
пространно. Наконец нет общих решений даже квадратного уравнения, а
отдельные случаи рассматриваются отдельно, и для каждого случая
выводится особый метод решения, так что самая существенная черта
современной А. – общность даваемых ею решений – еще
совершенно отсутствует в начале XVI века.
Решение уравнений 3-ей и 4-ой степени
В
1505 году Сципион Феррео впервые решил один частный случай
кубического уравнения. Это решение однако не было им опубликовано, но
было сообщено одному ученику – Флориде. Последний, находясь в
1535 году в Венеции, вызвал на состязание уже известного в то время
математика Тарталью из Брешии и предложил ему несколько вопросов, для
разрешения которых нужно было уметь решать уравнения третьей степени.
Но Тарталья уже нашел раньше сам решение таких уравнений и, мало
того, не только одного того частного случая, который был решен
Феррео, но и двух других частных случаев. Тарталья принял вызов и сам
предложил Флориде также свои задачи. Результатом состязания было
полное поражение Флориде. Тарталья решил предложенные ему задачи в
продолжение двух часов, между тем как Флориде не мог решить ни одной
задачи, предложенной ему его противником (число предложенных с обеих
сторон задач было 30). Тарталья продолжал, подобно Феррео, скрывать
свое открытие, которое очень интересовало Кардано, профессора
математики и физики в Милане. Последний готовил к печати обширное
сочинение об арифметике, алгебре и геометрии, в котором он хотел дать
также решение уравнений 3-ей степени. Но Тарталья отказывался
сообщить ему о своем способе. Только когда Кардано поклялся над
Евангелием и дал честное слово дворянина, что он не откроет способа
Тартальи для решения уравнений и запишет его в виде непонятной
анаграммы, Тарталья согласился, после долгих колебаний, раскрыть свою
тайну любопытному математику и показал ему правила решений кубических
уравнений, изложенные в стихах, довольно туманно. Остроумный Кардано
не только понял эти правила в туманном изложении Тартальи, но и нашел
доказательства для них. Не взирая, однако, на данное им обещание, он
опубликовал способ Тартальи, и способ этот известен до сих пор под
именем "формулы Кардано".
Вскоре
было открыто и решение уравнений четвертой степени. Один итальянский
математик предложил задачу, для решения которой известные до той поры
правила были недостаточны, а требовалось умение решать биквадратные
уравнения. Большинство математиков считало эту задачу неразрешимою.
Но Кардано предложил ее своему ученику Луиджи Феррари, который не
только решил задачу, но и нашел способ решать уравнения четвертой
степени вообще, сводя их к уравнениям третьей степени. В сочинении
Тартальи, напечатанном в 1546 году, мы также находим изложение
способа решать не только уравнения первой и второй степени, но и
кубические уравнения, причем рассказывается инцидент между автором и
Кардано, описанный выше. Сочинение Бомбелли, вышедшее в 1572 г.,
интересно в том отношении, что рассматривает так называемый
неприводимый случай кубического уравнения, который приводил в
смущение Кардано, не сумевшего решить его посредством своего правила,
а также указывает на связь этого случая с классическою задачей о
трисекции угла.
Развитие алгебры в странах Европы
В
Германии первое сочинение об алгебре принадлежит Христиану Рудольфу
из Иayepa, и появилось впервые в 1524 г. а затем вновь издано
Стифелем в 1571 г. Сам Стифель и Шейбль, независимо от итальянских
математиков, разработали некоторые алгебраические вопросы.
В
Англии первый трактат об алгебре принадлежит Роберту Рекорду,
преподавателю математики и медицины в Кембридже. Его сочинение об
алгебре называется "The Whetstone of Wit". Здесь впервые
вводится знак равенства (=). Во Франции в 1558 году появилось первое
сочинение об алгебре, принадлежащее Пелетариусу; в Голландии Стевин в
1585 г. не только изложил исследования, известные уже до него, но и
ввел некоторые усовершенствования в алгебру. Например, он уже
обозначал неизвестные. Правда, для обозначения неизвестных он
использовал всего лишь числа, обведенные в кружочек. Так первая
неизвестная (теперь обычно обозначаемая x)
у него обозначалась обведенной в кружочек единицей, вторая –
обведенной двойкой, и так далее. Громадные успехи сделала алгебра
после сочинений Виета, который первый рассмотрел общие свойства для
уравнений произвольных степеней и показал способы для
приблизительного нахождения корней каких бы то ни было алгебраических
уравнений. Он же первый обозначил величины, входящие в уравнения
буквами, и тем придал алгебре ту общность, которая составляет
характеристическую особенность алгебраических исследований нового
времени. Он же подошел весьма близко к открытию формулы бинома,
найденной впоследствии Ньютоном, и, наконец, в его сочинениях можно
даже встретить разложение отношения стороны квадрата вписанного в
круг к дуге круга, выраженное в виде бесконечного произведения.
Фламандец Албер Жирар или Жерар, трактат которого об алгебре появился
в 1629 г. первый ввел понятие мнимых величин в науку. Агличанин
Гарриот показал, что всякое уравнение может рассматриваться, как
произведение некоторого числа множителей первого порядка, и ввел в
употребление знаки > и <. Его труды были опубликованы в 1631 г.
Варнером.
Приобретение алгеброй законченного вида
После
этих сравнительно незначительных успехов алгебра вдруг движется
быстрыми шагами вперед, благодаря работам Декарта, Фермата, Валлиса и
в особенности Ньютона, не говоря уже о множестве математиков менее
знаменитых, но все же подвинувших совокупными усилиями алгебру в
течение сравнительно короткого времени на значительную степень выше
их предшественников и придавших ей ту форму, которую она сохранила до
настоящего времени. Нет возможности в этом кратком очерке обозреть
успехи, которым алгебра обязана названным математикам. Мы вкратце
только упомянем о главных пунктах дальнейшего быстрого
совершенствования алгебры, шедшего шаг за шагом за совершенствованием
иных отраслей математики вообще. С этого времени также алгебра входит
в более тесную связь с геометрией, после разработки Декартом
аналитической геометрии, а также с анализом бесконечно малых,
изобретенным Ньютоном и Лейбницем. В XVIII столетии классические
труды Эйлера и Лагранжа, изложенные в "Novi Commentarii"
первого и в "Traite de la resolution des equations"
второго, довели алгебру до высокой степени совершенства. Позже работы
Гаусса, Абеля, Фурье, Галуа, Коши, а затем Кейли, Сильвестера,
Кронекера, Эрмита и др. создали новые точки зрения на важнейшие
алгебраические вопросы и придали алгебре высокую степень изящества и
простоты.
Что изучает геометрия?
Многие предметы имеют прямоугольную форму, другие круглую, третьи - треугольную. Бывают и более сложные формы.
Если посмотреть более внимательно, то можно заметить, что тот же прямоугольник состоит из четырех отрезков, которые образуют его стороны. Т. е. можно сказать, что большинство фигур состоит из более простых фигур. Все фигуры состоят из точек. Поэтому точку можно считать простейшим элементом.
При описании фигур важно ни только указать геометрические примитивы, из которых она состоит, но и "отношения" между ними. Например, прямоугольник не просто состоит из четырех отрезков, но они должны быть соединены между собой; углы, образуемые соединенными отрезками, должны быть прямыми; кроме того отрезки должны быть попарно равны, и отрезки с одинаковой длинной располагаться на противоположных сторонах.
В то же время прямоугольники бывают разными. Один более вытянутый по одной стороне и больше похожий на брусок, у другого ширина и длина не сильно отличаются, и такой прямоугольник похож на квадрат. Ну и понятно, прямоугольники могут различаться по своим размерам. Все это говорит о том, что под термином "прямоугольник" мы понимаем множество фигур, удовлетворяющих определенным требованиям.
Геометрия - древняя наука. Она возникла около 4-5 тыс. лет назад. Людям с древних времен требовалось измерять земельные участки, расстояния, различные предметы, делать замеры при постройке зданий. Слово «геометрия» в переводе с греческого означает «землемерие».
Сначала в истории накапливались правила различных геометрических построений. Потом в Древней Греции появились ученые, которые привнесли в геометрию много нового. В частности начали уделять большую роль рассуждениям, на основе которых можно было открыть новые факты и закономерности. Можно сказать, что геометрия как наука сформировалась к началу нашей эры.
Практическое значение геометрии велико. Кроме того, она учит человека рассуждать, видеть мир форм в их взаимосвязи и взаимодействии.
Наука геометрия делится на два больших раздела - планиметрию и стереометрию. Планиметрия изучает фигуры на плоскости. Это прямоугольники, треугольники, окружности, трапеции, иные четырехугольники. Стереометрия изучает фигуры в трехмерном пространстве. Это шар, куб, цилиндр, пирамида и многие другие.























Немає коментарів:
Дописати коментар